一篇把 mmWave Studio 参数“讲透”的 FMCW 雷达配置(原理篇)#
==!本内容仅个人学习中的记录,不敢保证正确性,请大佬轻喷,指点==
1. 参数概览:可调项、示例配置、基本原理#
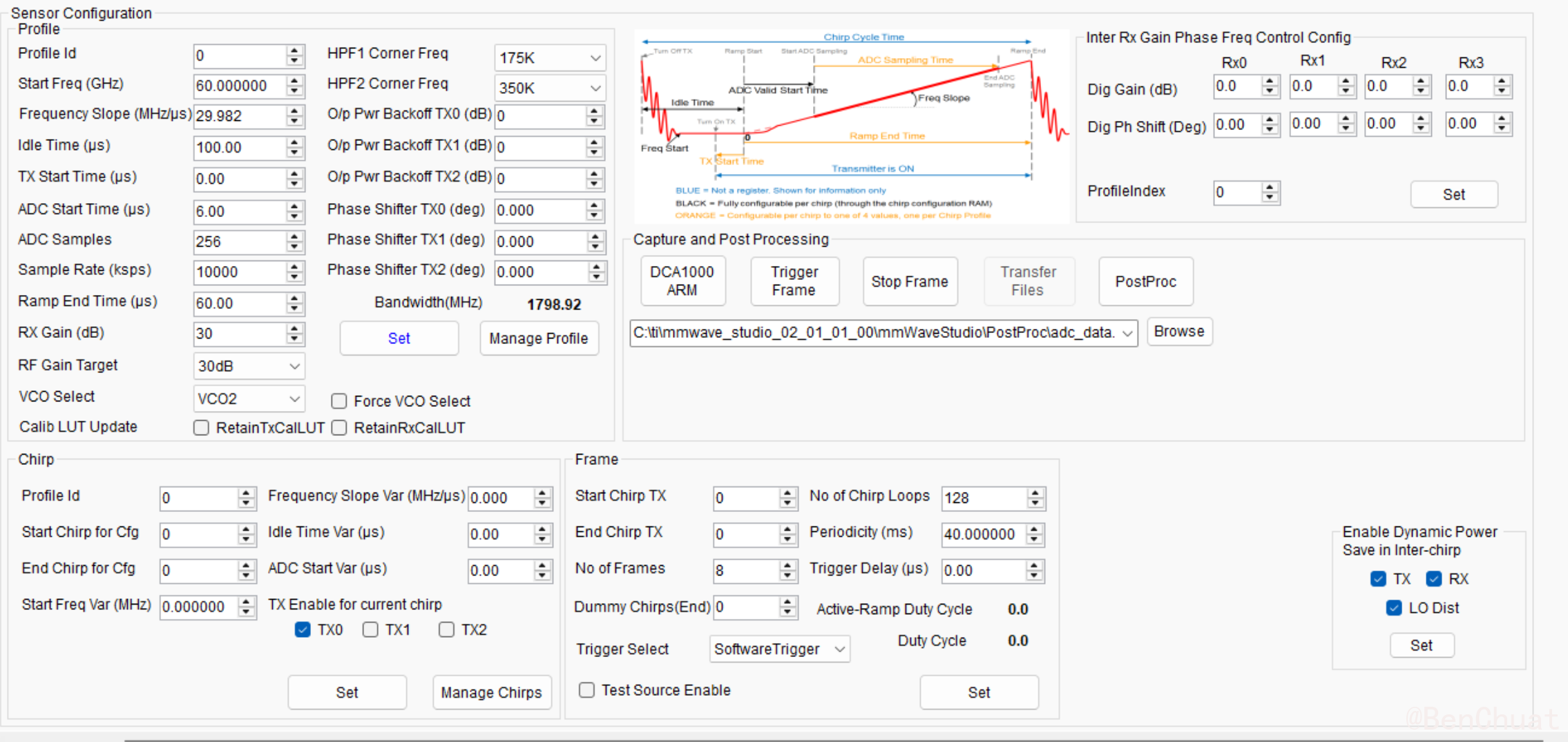
1.1 哪些参数可调?示例参数是什么?#
(1) Profile(单条 chirp 的“物理形状”和采样)
- 频率/扫频:Start Freq $f_0$,Frequency Slope $S$,Ramp End Time $T_\text{ramp}$(决定 Bandwidth $B$)
- 时序:Idle Time $T_\text{idle}$,ADC Start Time $T_\text{ADCstart}$
- 采样:ADC Samples $N_s$,Sample Rate $F_s$
- 链路:HPF1/HPF2(高通截止),RX Gain,TX backoff(每路 TX),Phase Shifter(每路 TX)
(2) Chirp(对每条 chirp 做微调)
- Start Freq Var、Frequency Slope Var、Idle Time Var、ADC Start Var(当前示例都为 0)
(3) Frame(把 chirp 组织成帧/序列)
- No of Chirp Loops $N_\text{chirp}$,Periodicity $T_\text{frame}$,No of Frames $N_\text{frame}$,Trigger Delay,Dummy Chirps(End)
当前截图示例(基准配置 A)
- $f_0=60\,\text{GHz}$,$S=29.982\,\text{MHz}/\mu s$,$T_\text{ramp}=60\,\mu s$
- $T_\text{idle}=100\,\mu s$,$T_\text{ADCstart}=6\,\mu s$
- $N_s=256$,$F_s=10\,\text{Msps}$
- HPF1/HPF2:175kHz / 350kHz
- RX Gain=30dB,TX backoff=0dB,仅 TX0 使能
- $N_\text{chirp}=128$,$T_\text{frame}=40\,\text{ms}$,$N_\text{frame}=8$
1.2 基本原理一句话(够用即可)#
- FMCW 线性 chirp:$f(t)=f_0+St$
- 带宽:$B=S\,T_\text{ramp}$,距离分辨率:$\Delta R=\frac{c}{2B}$
- 采样窗:$T_\text{sampling}=\frac{N_s}{F_s}$,并需满足 $T_\text{ramp} > T_\text{ADCstart}+T_\text{sampling}+T_\text{excess}$
- 单 chirp 周期:$T_c=T_\text{idle}+T_\text{ramp}$,帧内有效时长:$T_\text{active}=N_\text{chirp}T_c$,帧间空闲:$T_\text{IFidle}=T_\text{frame}-T_\text{active}$
2. 距离分辨率与距离谱质量#
2.0 先解释几个名词:距离分辨率、距离谱(Range FFT)、带宽#
- 距离分辨率 $\Delta R$(Range Resolution)
表示雷达在“距离方向”能分开两个目标的最小间隔。
现实含义:两个物体如果相距小于 $\Delta R$,在距离谱里往往会“糊在一起”变成一个峰;相距大于 $\Delta R$,更可能出现两个可分辨的峰。 - 距离谱(Range Profile / Range FFT)
对每条 chirp 的快时间采样做 FFT 得到的频谱,再按“拍频 $\rightarrow$ 距离”的映射换算成距离轴。
现实含义:距离谱上的每一个峰,通常对应某个距离处的散射体(目标或反射面)。峰越尖、旁瓣越低,越容易判断真实目标位置。 - 带宽 $B$(Bandwidth)
一条 chirp 在 ramp 期间扫过的频率范围。
现实含义:带宽越大,距离分辨率越好;就像相机的“分辨率”更高,能看清更细的距离结构。
2.1 距离分辨率($\Delta R$)#
2.1.1 参数如何影响测距(原理)#
核心链路:$S$ 与 $T_\text{ramp}$ 决定 $B$,$B$ 决定 $\Delta R$
$$ B=S\,T_\text{ramp} $$$$ \Delta R=\frac{c}{2B} $$基准配置 A:
$$ B=29.982\times 60=1798.92\,\text{MHz} $$$$ \Delta R\approx \frac{3\times10^8}{2\times1.79892\times10^9}\approx 0.083\,\text{m} $$直觉:$S$ 或 $T_\text{ramp}$ 增大 → 带宽增大 → 距离分辨率更好;但过大的 $S$ 会推高拍频,对采样率/模拟带宽更苛刻(见第 3 节)。
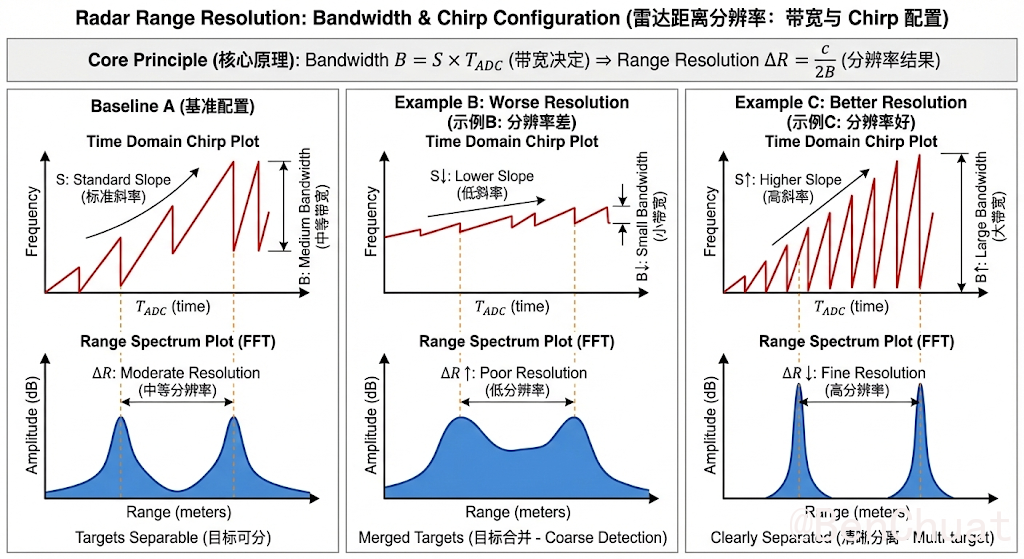
2.1.2举例两组不同的数据#
示例 B(分辨率更差):$S=15\,\text{MHz}/\mu s$,$T_\text{ramp}=60\,\mu s$
$$ B=15\times60=900\,\text{MHz},\quad \Delta R\approx \frac{3\times10^8}{2\times9\times10^8}=0.167\,\text{m} $$示例 C(分辨率更好):$S=40\,\text{MHz}/\mu s$,$T_\text{ramp}=60\,\mu s$
$$ B=40\times60=2400\,\text{MHz},\quad \Delta R\approx \frac{3\times10^8}{2\times2.4\times10^9}=0.0625\,\text{m} $$2.2 应用场景#
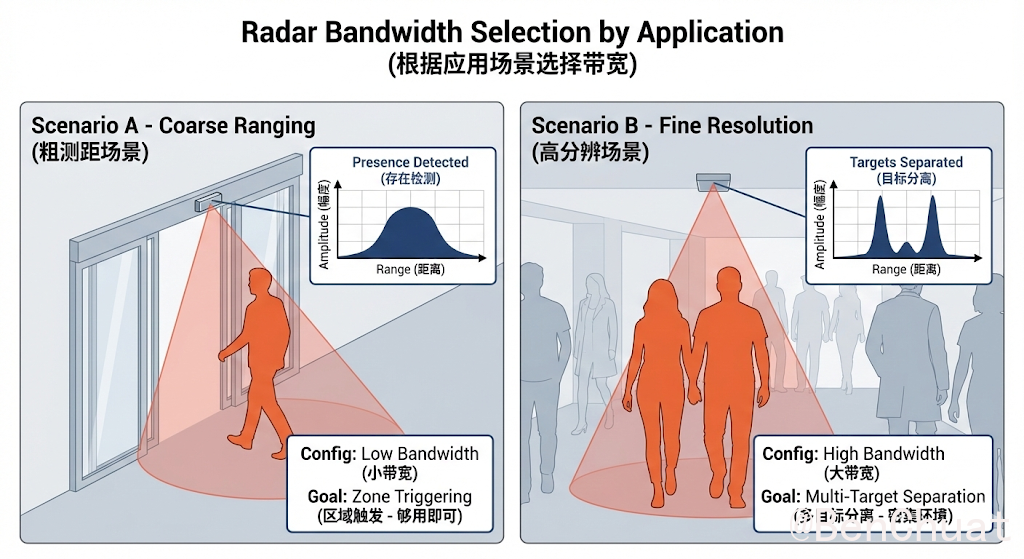
- 多目标分离(近距离多个散射点/多人/反射体密集):优先提高 $B$(提升 $\Delta R$)。
- 只需粗测距(存在检测/区域触发):$B$ 够用即可,把预算留给帧率与稳定性。
3. 最大测距与距离混叠(量程、折叠、假峰)#
3.0 先解释几个名词:拍频、混叠、无混叠距离#
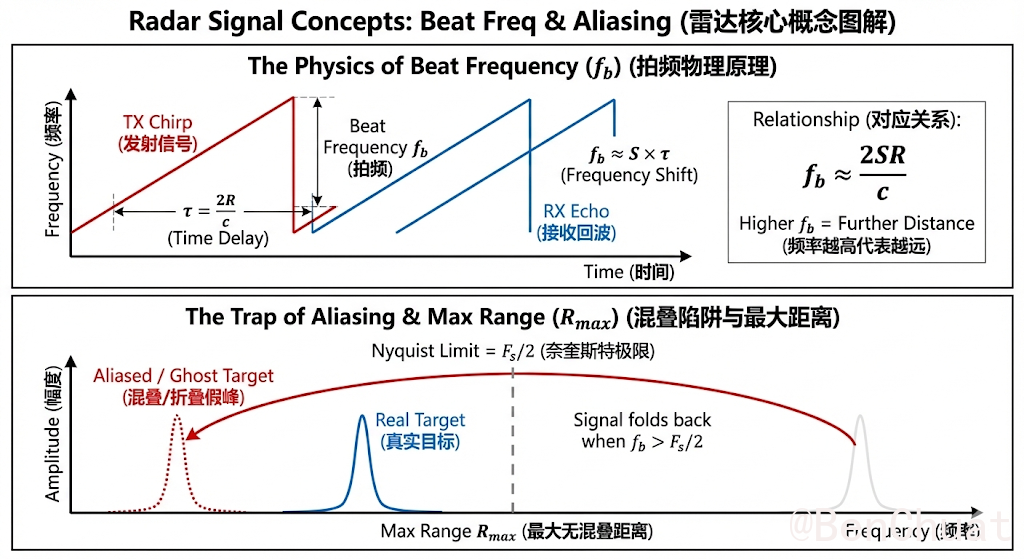
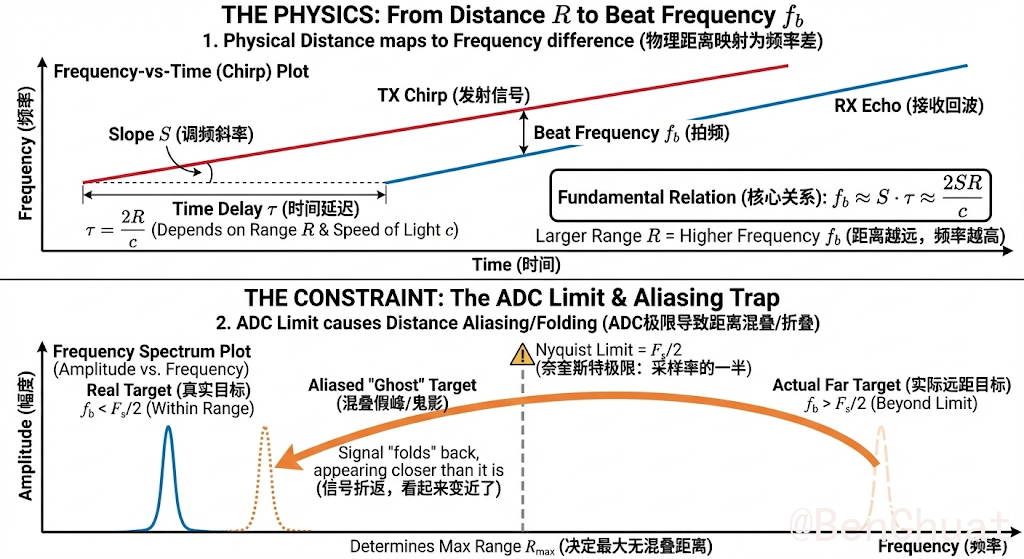
拍频 $f_b$(Beat Frequency)
FMCW 雷达把“发射 chirp”和“目标回波”做混频(相当于两条频率很接近的信号相乘),输出一个低频信号,其主频率就是拍频 $f_b$。
现实含义:拍频越高,通常代表目标越远(在静止目标情况下),因为回波延迟更大。(静止目标)拍频与距离的对应
$$ f_b\approx S\tau=\frac{2SR}{c} $$
目标距离 $R$ 造成往返时延 $\tau=\frac{2R}{c}$,在扫频斜率为 $S$ 时,回波相对发射的“频率错位”约为 $S\tau$,因此静止目标拍频近似:现实含义:同一套配置下,你看到的“拍频谱峰值位置”可以直接换算成距离。
混叠(Aliasing)/ 折叠
ADC 以采样率 $F_s$ 采样时,能够正确表示的最高频率大约是 $F_s/2$(Nyquist)。如果拍频超过这个上限,频谱会“折回”到低频区,看起来像一个假的低拍频峰。
现实含义:远处目标可能被“折叠”到近处,形成假峰或距离跑偏。最大无混叠距离 $R_\text{max}$
就是“拍频刚好不超过 $F_s/2$ 时对应的最大距离”。超过它的目标可能产生折叠。
3.1 最大无混叠距离($R_\text{max}$)#
3.1.1 参数如何影响量程(原理)#
静止目标拍频近似:
$$ f_b\approx \frac{2SR}{c} $$采样率决定最大可采拍频(Nyquist):
$$ f_{b,\max}\approx \frac{F_s}{2} $$映射到最大无混叠距离(常用估算):
$$ R_\text{max}\approx \frac{c}{2S}\cdot\frac{F_s}{2}=\frac{cF_s}{4S} $$基准配置 A($F_s=10\,\text{Msps}$,$S=29.982\,\text{MHz}/\mu s$):
$$ R_\text{max}\approx \frac{3\times10^8\times10\times10^6}{4\times29.982\times10^{12}}\approx 25\,\text{m} $$直觉:提高 $F_s$ 增量程;提高 $S$ 减量程(用分辨率换量程)。
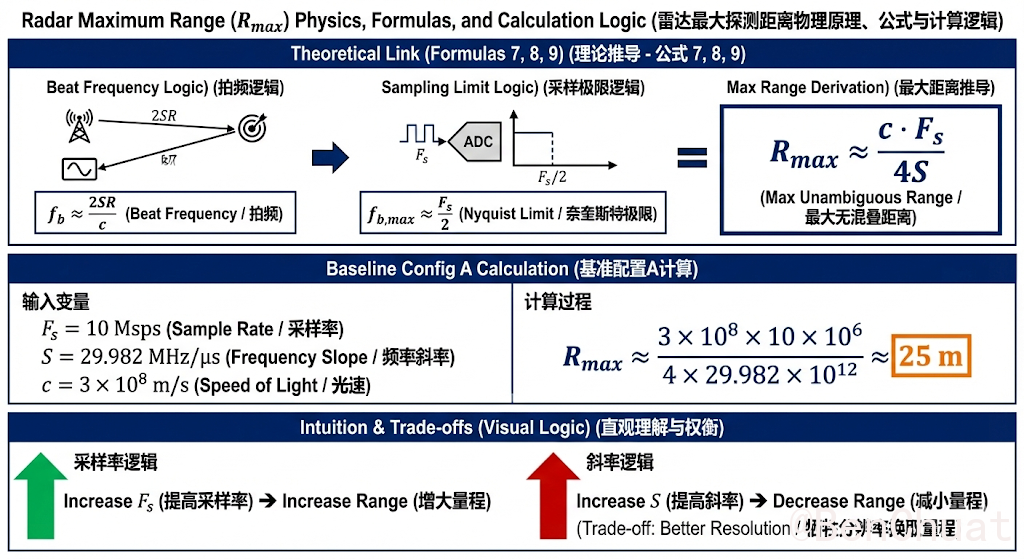
3.1.2(举例)两组不同的数据#
示例 D(降低采样率,量程下降):$F_s=5\,\text{Msps}$,$S$ 同 A
$$ R_\text{max}\approx \frac{3\times10^8\times5\times10^6}{4\times29.982\times10^{12}}\approx 12.5\,\text{m} $$示例 E(降低斜率,量程显著增大):$S=10\,\text{MHz}/\mu s$,$F_s=10\,\text{Msps}$
$$ R_\text{max}\approx \frac{3\times10^8\times10\times10^6}{4\times10\times10^{12}}\approx 75\,\text{m} $$3.2 应用场景#
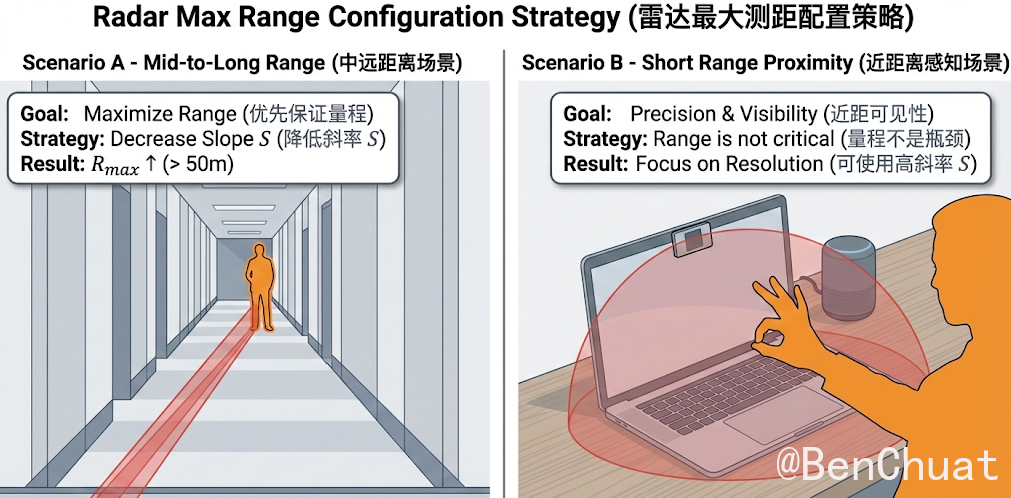
- 中远距离测距(走廊/道路/大空间):优先保证 $R_\text{max}$(降低 $S$ 或提高 $F_s$)。
- 近距离感知(桌面/人体近距):量程不是瓶颈,更重要的是近距可见性和不过载(见第 5、6 节)。
4. 测速与运动解析(无模糊速度、速度分辨率、帧内 chirp 数)#
4.0 先解释几个名词:多普勒、无模糊速度、速度分辨率#
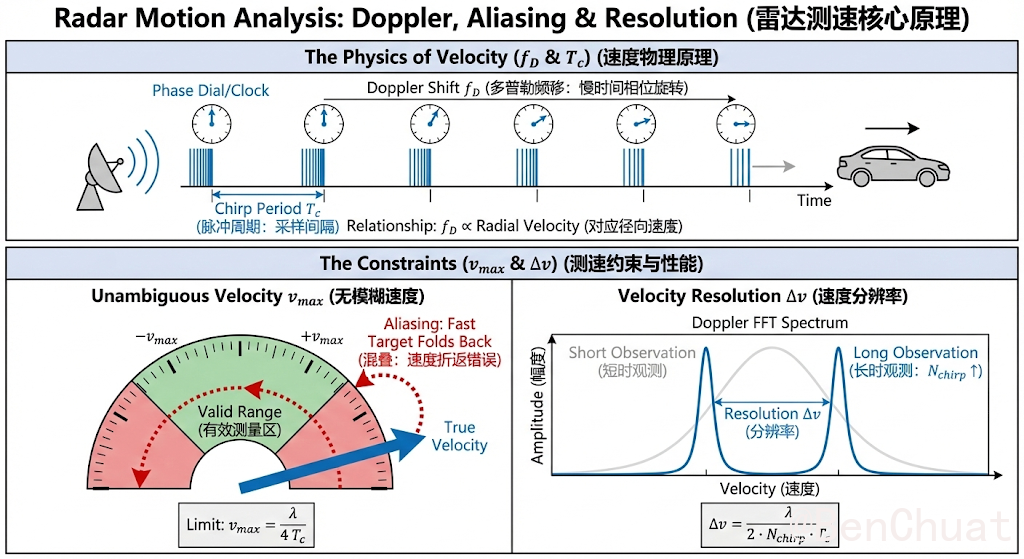
多普勒频移 $f_D$(Doppler Shift)
目标在径向方向运动时,回波会产生频率偏移(类似救护车鸣笛靠近/远离时音调变化)。
现实含义:你在数据里看到的“慢时间上的相位旋转/频率偏移”对应目标的径向速度。chirp 周期 $T_c$(Chirp Repetition Interval)
相邻两条 chirp 的时间间隔,通常由 $T_\text{idle}+T_\text{ramp}$ 构成。
现实含义:雷达“多普勒采样”的采样间隔。$T_c$ 越小,速度采样越密。无模糊速度 $v_\text{max}$(Unambiguous Velocity)
由于速度是在“离散时间采样(每隔 $T_c$ 采一次)”下估计的,速度也会像频率一样发生混叠。
现实含义:当目标速度超过 $v_\text{max}$ 时,估计的速度会折叠到一个错误的速度值(看起来变慢或方向错)。速度分辨率 $\Delta v$(Velocity Resolution)
一帧内用 $N_\text{chirp}$ 条 chirp 做 Doppler FFT,相当于观测时长约为 $N_\text{chirp}T_c$。观测越久,频率(速度)分辨越细。
现实含义:$\Delta v$ 越小,你越能分开两个接近的速度(或把慢速变化测得更细)。
4.1 速度无模糊范围($v_\text{max}$)与速度分辨率($\Delta v$)#
4.1.1 参数如何影响测速(原理)#
单 chirp 周期:
$$ T_c=T_\text{idle}+T_\text{ramp} $$载波波长(以 $f_c\approx 60\,\text{GHz}$ 为例):
$$ \lambda=\frac{c}{f_c}\approx \frac{3\times10^8}{60\times10^9}=0.005\,\text{m} $$常用近似(单 TX、等间隔 chirp):
$$ v_\text{max}\approx \frac{\lambda}{4T_c} $$若一帧使用 $N_\text{chirp}$ 条 chirp 做 Doppler FFT:
$$ \Delta v\approx \frac{\lambda}{2N_\text{chirp}T_c} $$基准配置 A:$T_c=100+60=160\,\mu s$,$N_\text{chirp}=128$
$$ v_\text{max}\approx \frac{0.005}{4\times160\times10^{-6}}\approx 7.81\,\text{m/s} $$$$ \Delta v\approx \frac{0.005}{2\times128\times160\times10^{-6}}\approx 0.122\,\text{m/s} $$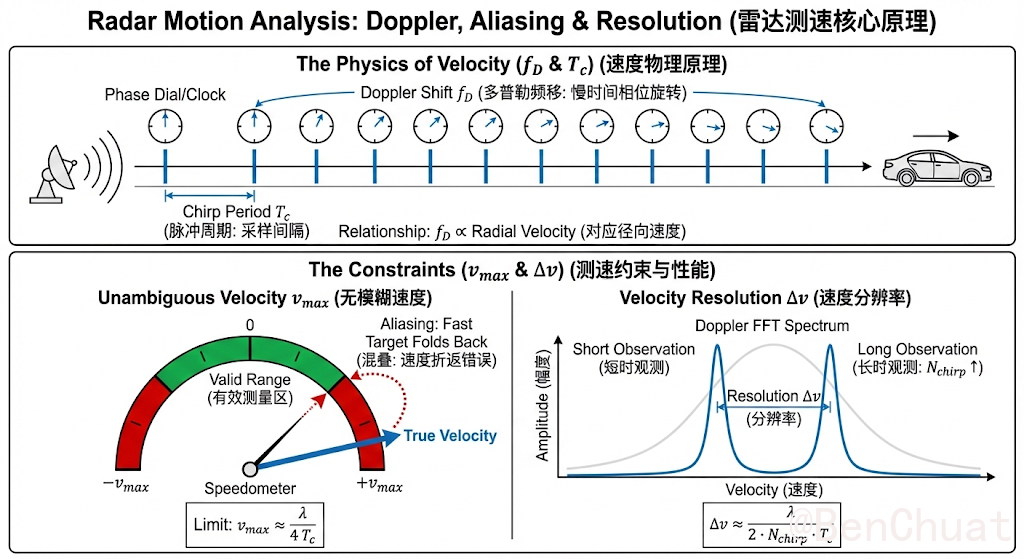
4.1.2(举例)两组不同的数据#
示例 F(提高 $v_\text{max}$:减小 Idle):$T_\text{idle}=40\,\mu s$,$T_\text{ramp}=60\,\mu s\Rightarrow T_c=100\,\mu s$
$$ v_\text{max}\approx \frac{0.005}{4\times100\times10^{-6}}=12.5\,\text{m/s} $$示例 G(提高 $\Delta v$ 分辨率:增大 loops):$N_\text{chirp}=256$,$T_c$ 同 A
$$ \Delta v\approx \frac{0.005}{2\times256\times160\times10^{-6}}\approx 0.061\,\text{m/s} $$4.2 应用场景#
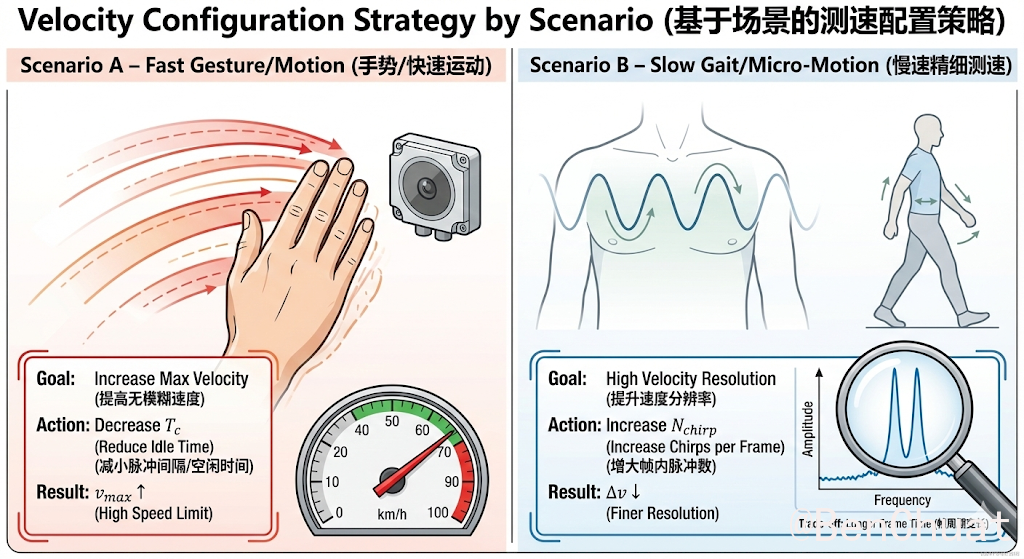
- 手势/快速运动:优先提高 $v_\text{max}$(减小 $T_c$,主要靠减 Idle)。
- 慢速精细测速(步态、细微运动):增大 $N_\text{chirp}$ 提升速度分辨率,但会压缩帧周期预算(见第 7 节)。
5. 近距离可见性与静态杂波(HPF 对“近距”和泄漏的影响)#
5.0 先解释几个名词:泄漏、静态杂波、HPF 截止频率#
泄漏(TX-RX Leakage / Self-Interference)
发射端与接收端之间会存在直接耦合(天线隔离不完美、板级走线耦合等),即使前方没有目标,接收端也会看到一个很强的“自干扰”分量,通常集中在直流/极低频附近。
现实含义:你会在距离谱最靠前(近零距离)看到很强的能量,甚至抬高整个噪声底。静态杂波(Static Clutter)
环境中不动的物体(墙、桌面、地面、固定支架)产生稳定回波。对 FMCW 而言,这些回波也会在拍频域形成稳定分量,尤其在低拍频区域能量很大。
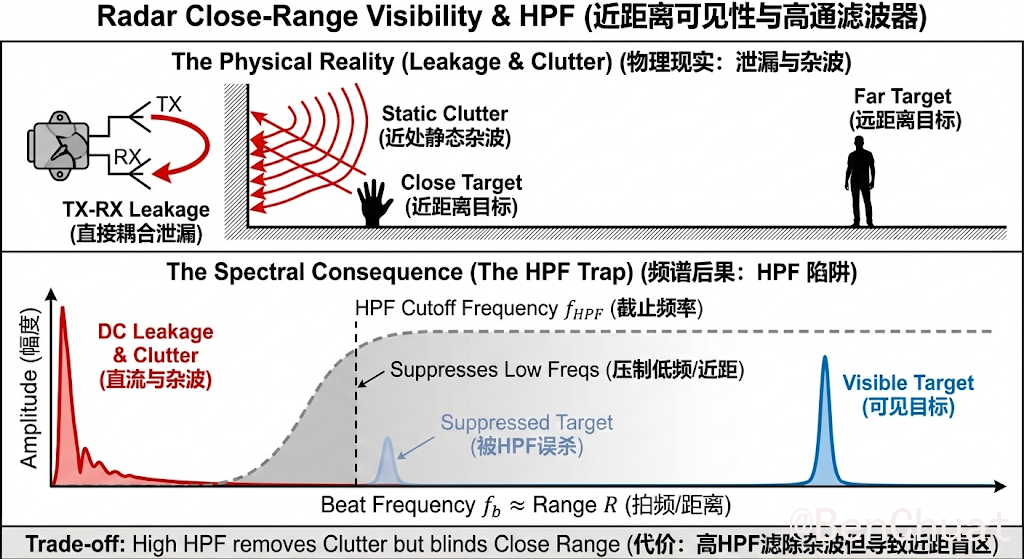
现实含义:如果你只想看运动目标或远处目标,静态背景会把低频区“糊住”。高通滤波器 HPF 与截止频率 $f_\text{HPF}$
HPF 会衰减低于截止频率的拍频分量,用来压制泄漏与静态杂波。
现实含义:HPF 设得越高,低频(对应近距离、强泄漏、静态背景)压得越狠;但代价是近距离目标也会被一起压掉。“近距离为何会被 HPF 影响?”
$$ f_b\approx \frac{2SR}{c} $$
静止目标的拍频与距离近似成正比:距离越近,拍频越低,越容易落在 HPF 的抑制频段里。
5.1 HPF 对近距的“切除效应”#
5.1.1 参数如何影响近距离(原理)#
静止目标拍频:
$$ f_b\approx \frac{2SR}{c} $$若高通截止为 $f_\text{HPF}$,对应的“等效最小可见距离”近似:
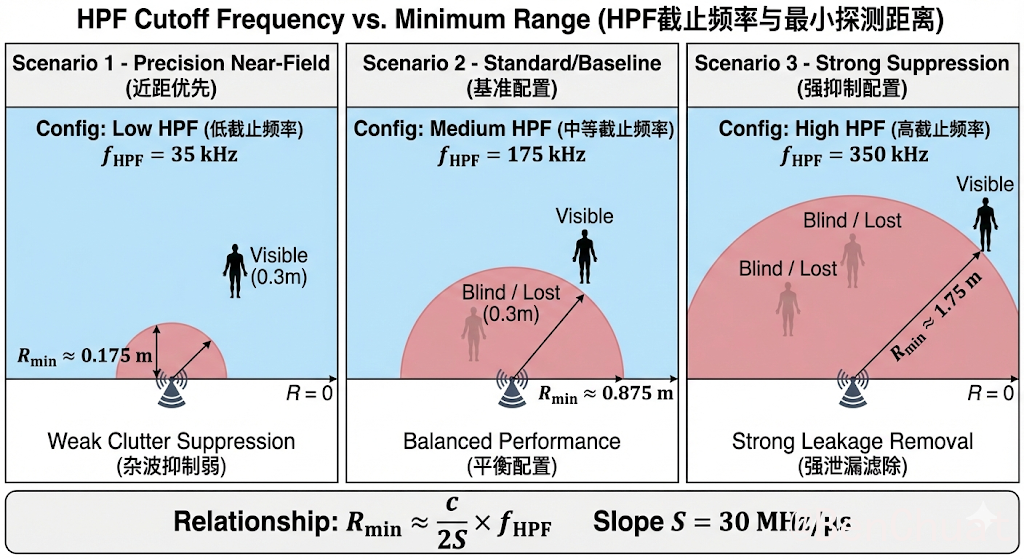
$$ R_{\min,\text{HPF}}\approx \frac{c}{2S}f_\text{HPF} $$基准配置 A($S=29.982\,\text{MHz}/\mu s$):
- HPF1=175kHz $$ R_{\min}\approx \frac{3\times10^8}{2\times29.982\times10^{12}}\times175\times10^3\approx 0.875\,\text{m} $$
- HPF2=350kHz $$ R_{\min}\approx 1.75\,\text{m} $$
直觉:HPF 越高,越能压 DC/泄漏/静态杂波,但越“看不见”近距离目标。
5.1.2(举例)两组不同的数据#
示例 H(更适合 0.3m 近距:降低 HPF):$f_\text{HPF}=35\,\text{kHz}$
$$ R_{\min}\approx \frac{3\times10^8}{2\times29.982\times10^{12}}\times35\times10^3\approx 0.175\,\text{m} $$示例 I(更强抑制近距/泄漏:提高 HPF):$f_\text{HPF}=700\,\text{kHz}$
$$ R_{\min}\approx 3.5\,\text{m} $$5.2 应用场景#
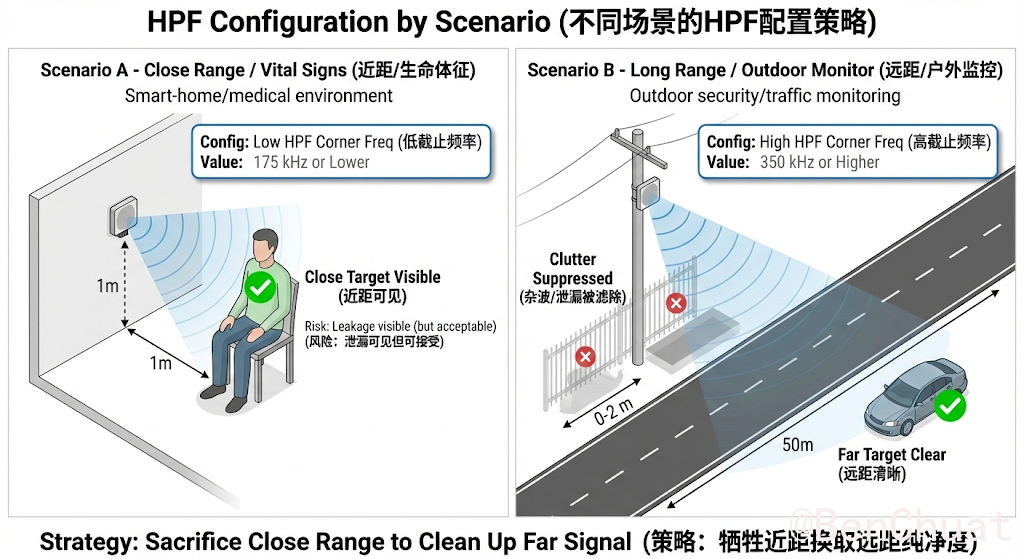
- 喉部/胸口/桌面近距(0–1m):HPF 建议尽量低,否则近距被显著衰减,易出现“远处多径假峰更显眼”。
- 远距离 + 强静态背景:可提高 HPF 抑制泄漏/静态杂波,牺牲近距无所谓。
6. 动态范围、SNR 与饱和(RX Gain / TX backoff)#
6.0 先解释几个名词:SNR、动态范围、饱和/削顶、非线性杂散#
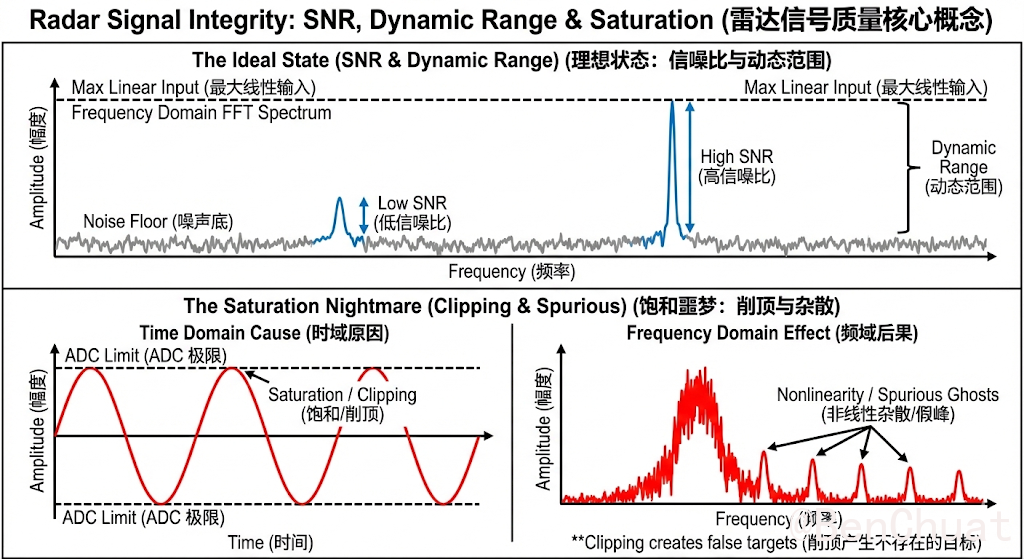
SNR(Signal-to-Noise Ratio,信噪比)
信号幅度相对于噪声底的强弱。
现实含义:SNR 越高,你在距离谱/多普勒谱里越容易把目标峰从噪声里“抠出来”;SNR 太低时目标会淹没在噪声底,表现为峰不稳定、检测不到。动态范围(Dynamic Range)
接收链路能同时处理的“最强信号”和“最弱信号”的跨度。
现实含义:场景里可能同时存在近距离强反射(很强)和远距离弱目标(很弱)。动态范围不够时,要么强信号把前端顶饱和,要么为了不饱和而把增益降太低导致弱目标看不见。饱和/削顶(Saturation / Clipping)
当前端放大器或 ADC 输入超过其可线性表示的范围,波形被“截平”。
现实含义:距离谱会出现异常的宽底噪、假峰、旁瓣异常;相位会突变,微动/测速也会变得不可信。非线性与杂散(Nonlinearity / Spurious)
在饱和或接近饱和时,系统产生谐波、互调等非线性产物,映射到频谱里就是额外的“假峰/条纹”。
现实含义:你可能会看到并不存在的目标峰,或者真实峰被污染难以判断。TX backoff 与 RX Gain 的直觉角色
- TX backoff 本质是在“源头”把发射功率压下去,减少进入接收机的强回波/泄漏。
- RX Gain 是在“接收端”把信号整体放大,既放大目标也放大噪声与干扰。
6.1 为什么会饱和?如何用参数控制?#
6.1.1 参数如何影响(原理)#
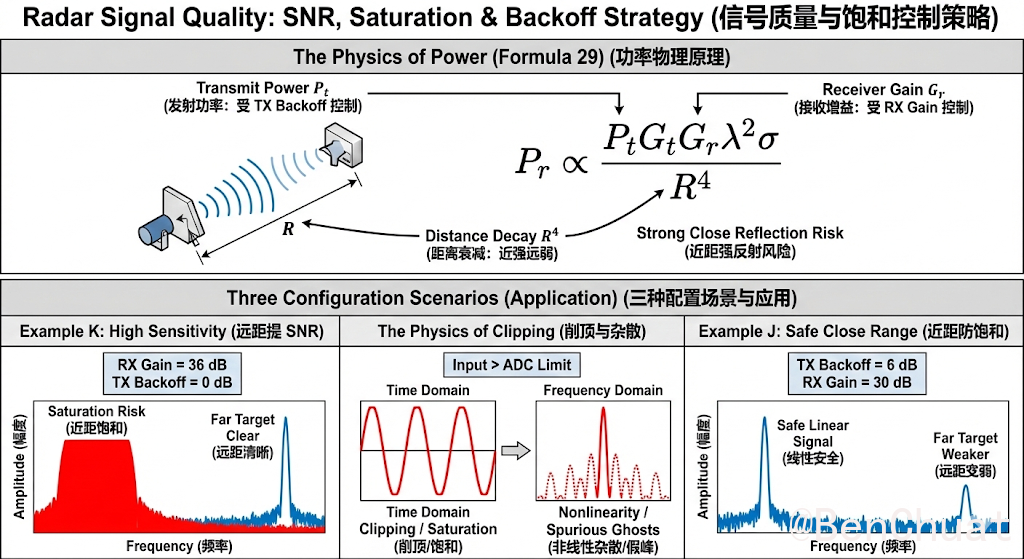
回波强度随 $R$ 迅速衰减(趋势可由雷达方程理解):
$$ P_r \propto \frac{P_t\,G_t\,G_r\,\lambda^2\,\sigma}{R^4} $$- TX backoff 增大 → $P_t$ 下降 → 回波变弱(SNR 下降),但饱和/非线性/杂散风险下降。
- RX Gain 增大 → ADC 输入变大(弱目标更容易看到),但强反射/近距泄漏时更容易削顶饱和。
6.1.2(举例)两组不同的数据#
示例 J(近距防饱和):TX backoff = 6 dB,RX Gain 仍 30 dB
- 近距离强反射时削顶风险明显降低;代价是远距离弱目标可能沉到噪声里。
示例 K(远距提 SNR):RX Gain = 36 dB,TX backoff 仍 0 dB
- 远距弱目标更清晰;代价是遇到近距强反射更容易饱和,距离谱出现假峰/底噪抬升。
6.2 应用场景#
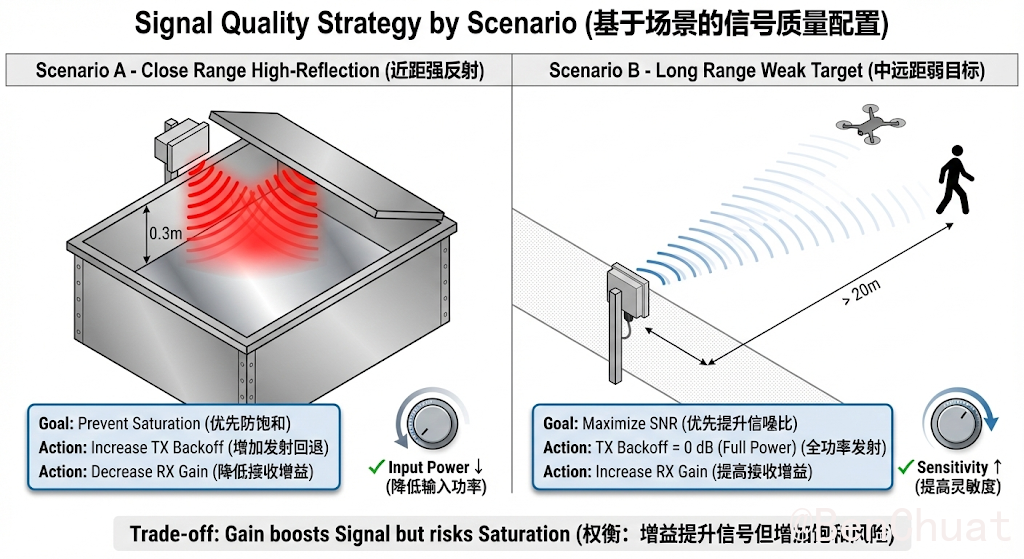
- 近距离(<1m):优先不饱和(适当降低 RX Gain 或增加 TX backoff)。
- 中远距离弱目标:优先 SNR(适当提高 RX Gain,前提是不饱和)。
7. 时序可行性与实时性(采样窗约束、帧周期约束、数据率)#
7.0 先解释几个名词:采样窗、ramp、帧周期、帧内有效时间、数据率#
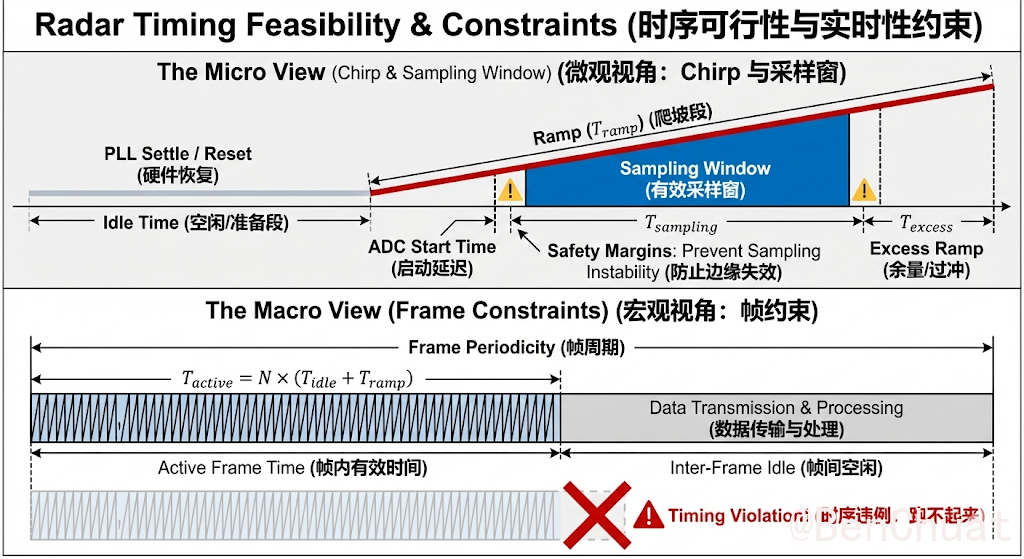
ramp(扫频段)与 Idle(空闲段)
一条 FMCW chirp 通常由“空闲/准备段(Idle)”+“线性扫频段(ramp)”组成。
现实含义:你只有在 ramp 的线性稳定区采到的 ADC 数据,才适合做距离 FFT;Idle 主要用于硬件恢复、PLL 稳定、时序对齐。采样窗(Sampling Window)
指 ADC 实际采样的那段时间,长度为 $T_\text{sampling}$,起点由 $T_\text{ADCstart}$ 决定。
现实含义:采样窗放得太靠前会吃到瞬态,太靠后会越过 ramp 末尾导致无效数据;采样窗的“摆放”直接决定数据能不能用、谱干不干净。Excess ramp(余量/过冲)$T_\text{excess}$
ramp 末尾预留的一小段不用于采样/用于留裕量的时间。
现实含义:防止采样贴边,给模拟链路、扫频非理想段留缓冲;忽略它容易导致“理论能装下,实际边缘失真”。帧周期(Frame Periodicity)$T_\text{frame}$
相邻两帧开始的时间间隔。
现实含义:决定帧率 $f_\text{frame}=1/T_\text{frame}$,直接影响实时性与刷新速度。帧内有效时间(Active Frame Time)$T_\text{active}$
一帧内真正发射/采集 chirp 的持续时间。
现实含义:如果 $T_\text{active}$ 已经接近甚至超过 $T_\text{frame}$,系统就没有帧间空闲来传输、处理或恢复,配置可能跑不起来或表现异常。数据率(Data Rate)
由采样率、采样点数、chirp 数、RX 通道数等共同决定。
现实含义:数据率过高会导致 DCA/链路丢包、缓存溢出、处理跟不上,表现为丢帧、数据断裂、谱不稳定。
7.1 两个最重要的“能不能跑”的约束#
7.1.1 参数如何影响(原理)#
(1) 采样窗必须装进 ramp
$$ T_\text{sampling}=\frac{N_s}{F_s} $$$$ T_\text{ramp} > T_\text{ADCstart}+T_\text{sampling}+T_\text{excess} $$(2) 帧周期必须装下帧内 burst
$$ T_c=T_\text{idle}+T_\text{ramp} $$$$ T_\text{active}=N_\text{chirp}T_c $$$$ T_\text{frame}\ge T_\text{active} $$基准配置 A:
$$ T_c=100+60=160\,\mu s $$$$ T_\text{active}=128\times160\,\mu s=20.48\,\text{ms} $$$T_\text{frame}=40\,\text{ms}$,满足 $40\ge 20.48$。
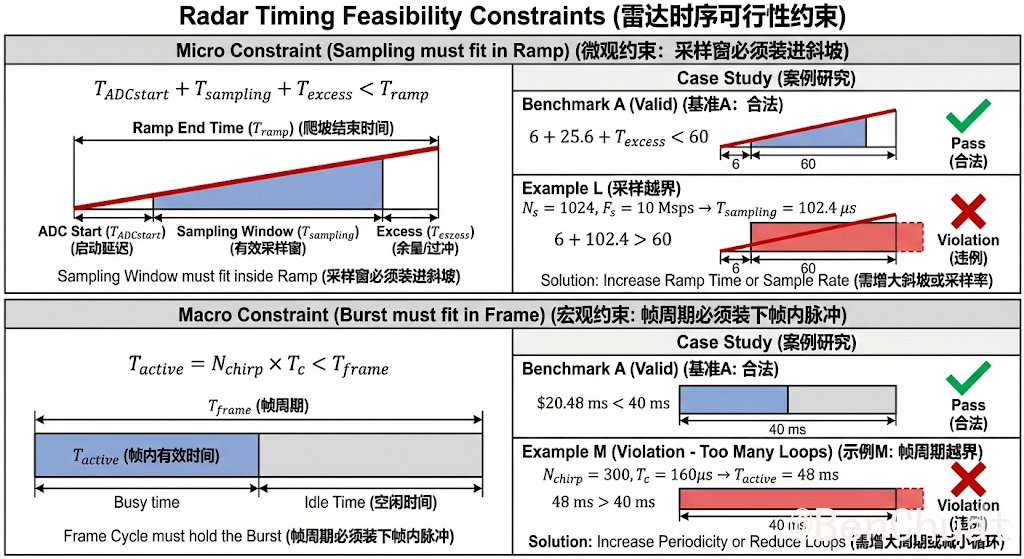
7.1.2(举例)两组不同的数据#
示例 L(采样点过多导致越界):$N_s=512$,$F_s=10\,\text{Msps}$,$T_\text{ADCstart}=10\,\mu s$
$$ T_\text{sampling}=\frac{512}{10\times10^6}=51.2\,\mu s $$$$ T_\text{ADCstart}+T_\text{sampling}=61.2\,\mu s>60\,\mu s $$→ 需要增大 $T_\text{ramp}$ 或提高 $F_s$ 或减小 $N_s$。
示例 M(loops 过大导致帧周期装不下):$N_\text{chirp}=256$,其余同 A
$$ T_\text{active}=256\times160\,\mu s=40.96\,\text{ms}>40\,\text{ms} $$→ 需要增大 $T_\text{frame}$ 或减小 $T_c$(减 Idle/减 ramp)或减 loops。
7.2 应用场景#
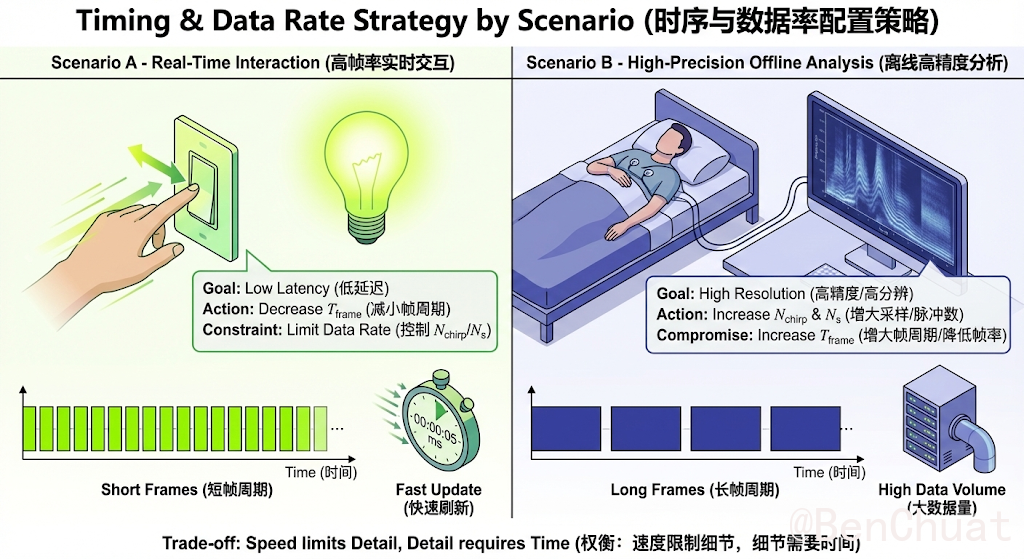
- 高帧率实时交互:减小 $T_\text{frame}$ 同时必须保证 $T_\text{frame}\ge T_\text{active}$,并控制数据率($N_s$、$N_\text{chirp}$ 别太大)。
- 离线高精度分析:可增大 $N_s$ 或 $N_\text{chirp}$,但同步增大 $T_\text{frame}$ 或缩短总帧数,避免系统带宽/存储爆炸。
8. 发射通道选择与MIMO 对速度的副作用(TX Enable)#
8.0 先解释几个名词:TX 通道、MIMO、TDM-MIMO、虚拟阵列#
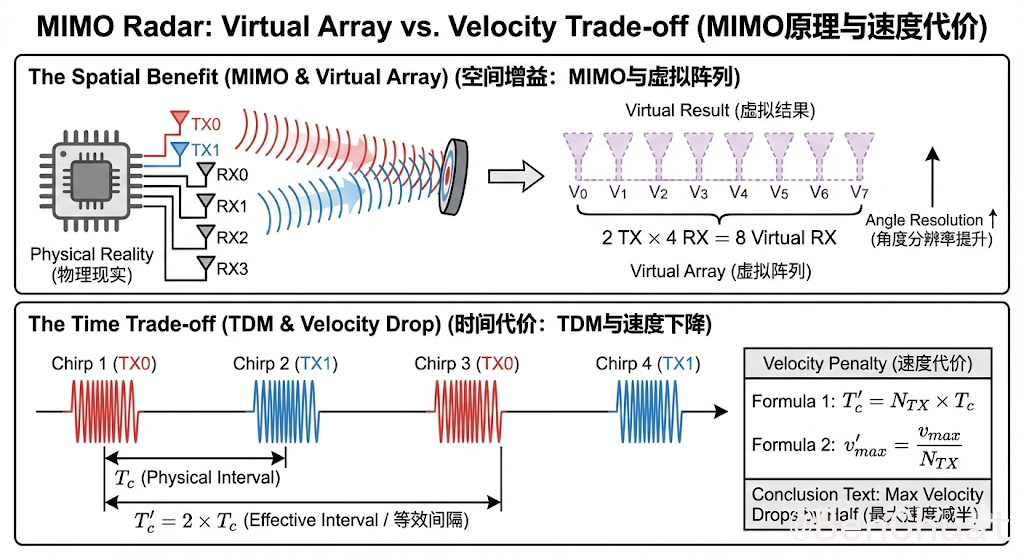
TX 通道(TX0/TX1/TX2)
雷达芯片通常有多路发射天线端口,每路 TX 对应一个物理发射天线或天线子阵。
现实含义:勾选哪些 TX,就决定“这一条 chirp 到底从哪些天线发射”,进而决定你能不能做角度估计、波束形成等。MIMO(Multiple-Input Multiple-Output)
用多路 TX 与多路 RX 的组合,形成更多“等效观测通道”。
现实含义:你能获得更大的等效孔径,从而提升角度分辨率、分离多目标角度、做更稳健的定位/跟踪。TDM-MIMO(Time-Division Multiplexing MIMO,时分 MIMO)
最常见实现方式:在不同 chirp 上轮流打开不同 TX(例如 TX0→TX1→TX2→TX0…),用“时间复用”来得到多发射通道信息。
现实含义:角度维度变强了,但代价是每个 TX 自己的“重复采样间隔”变大,速度无模糊范围会变小。虚拟阵列(Virtual Array)
把不同 TX-RX 组合看作不同的阵元位置,等效形成更多阵元的阵列。
现实含义:角度分辨率提高、旁瓣更可控,适合 AoA/定位/多目标分离。
8.1 TX Enable(TX0/TX1/TX2)怎么影响“你能做什么任务”#
8.1.1 参数如何影响(原理)#
- 只使能 TX0(截图)→ 单 TX:结构最简单,测速模型最直接。
- 若启用多 TX 做 TDM-MIMO,会让“同一 TX 的等效 chirp 间隔”变大,从而降低最大无模糊速度。粗略可用:
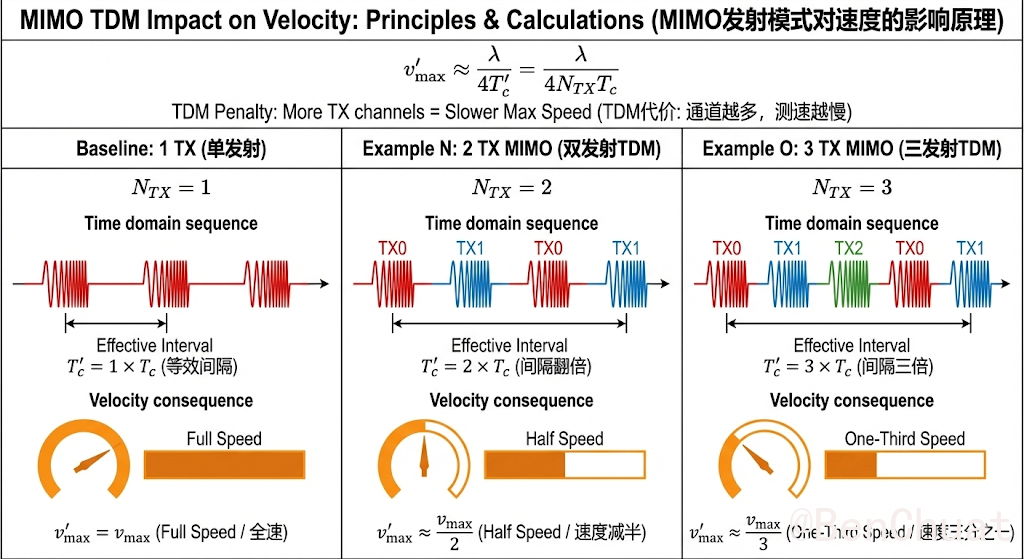
8.1.2(举例)两组不同的数据#
示例 N(开启 2TX 的 TDM):$N_\text{TX}=2$
$$ v_\text{max}'\approx \frac{v_\text{max}}{2} $$示例 O(开启 3TX 的 TDM):$N_\text{TX}=3$
$$ v_\text{max}'\approx \frac{v_\text{max}}{3} $$(换来角度维度/虚拟阵列的收益,但速度无模糊范围变小)
8.2 应用场景#
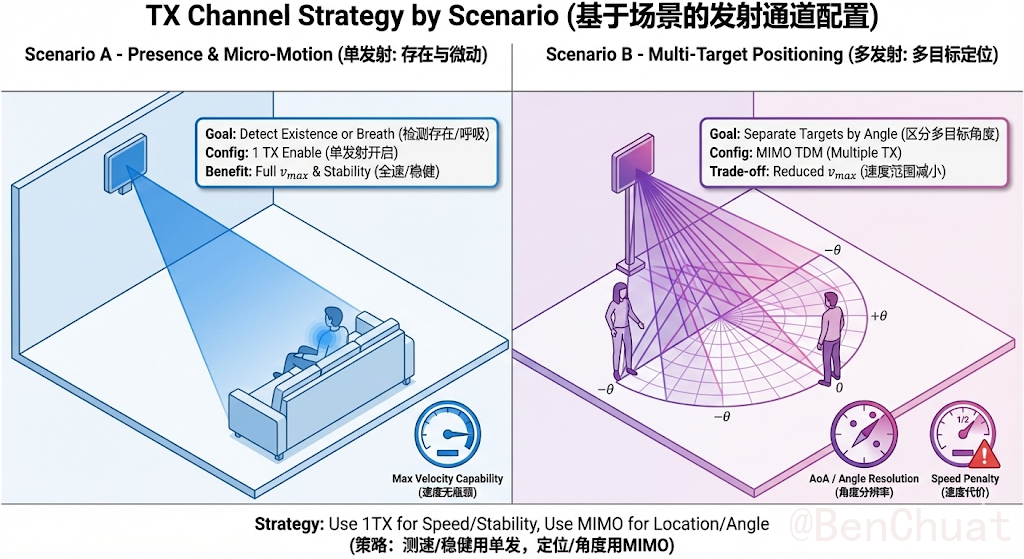
- 只做测距/微动/存在:单 TX 往往足够且更稳健。
- 需要角度/AoA(定位/多目标分离):启用多 TX/MIMO,但要重新评估 $v_\text{max}$ 与帧时序预算。
==!本内容仅个人学习中的记录,不敢保证正确性,请大佬轻喷,指点==
